Chapter 1 Recurrent Problems
Warmups
Homework exercises
1.8
List $Q_1$ through $Q_6$, we could find out that $Q$ is periodic.
$$\begin{aligned}Q_m&=\alpha;\\Q_{m+1}&=\beta;\\Q_{m+2}&=(1+\beta)/\alpha;\\Q_{m+3}&=(1+\alpha+\beta)/(\alpha\beta);\\Q_{m+4}&=(1+\alpha)/\beta,\quad\text{for $m\in\{0,5,10,\ldots\}$.}\end{aligned}$$
1.9a
$$\begin{aligned}x_1\ldots x_{n}&\leq\left(\frac{x_1+\cdots+x_{n-1}+x_n}{n}\right)^n\qquad\text{by $(n-1)x_n=x_1+\cdots+x_{n-1}$}\\x_1\ldots x_{n}&\leq\left(\frac{(n-1)x_n+x_n}{n}\right)^n\\x_1\ldots x_{n-1}&\leq(x_n)^{n-1}\\x_1\ldots x_{n-1}&\leq\left(\frac{x_1+\cdots+x_{n-1}}{n-1}\right)^{n-1}.\end{aligned}$$
1.9b
$$\begin{aligned}x_1\ldots x_n x_{n+1}\ldots x_{2n}&\leq\left(\frac{x_1+\cdots+x_n}{n}\right)^n\left(\frac{x_{n+1}+\cdots+x_{2n}}{n}\right)^n\qquad\text{by $P(2):x_1x_2\leq\left(\frac{x_1+x_2}2\right)^2$}\\&\leq\left(\frac{\left(\frac{x_1+\cdots+x_n+x_{n+1}+\cdots+x_{2n}}2\right)^2}{n^2}\right)^n\\&\leq\left(\frac{x_1+\cdots+x_n+x_{n+1}+\cdots+x_{2n}}{2n}\right)^{2n}.\end{aligned}$$
1.9c
For example, $P(5)$ follows from $P(6)$ from $P(3)$ from $P(4)$ from $P(2)$ which is proved to be true. And whenever $n>1$, $P(n)$ is finally based on $P(2)$.
1.10
It’s clear that $Q_n=2R_n-1$ if we
- move $n-1$ disks counter-clockwise;
- move the largest disk clockwise;
- move $n-1$ disks counter-clockwise again.
Then $R_n=2R_n+Q_{n-1}+2$ if we
- move $n-1$ disks counter-clockwise;
- move the largest disk clockwise;
- move $n-1$ disks clockwise;
- move the largest disk clockwise again;
- move $n-1$ disks back counter-clockwise.
Plug $Q_n=2R_n-1$ in, then $R_n=Q_n+Q_{n-1}+1$.
1.11a
Move a double $(n-1)$-tower, then move the two largest disks, which takes $2$ moves, then move the double $(n-1)$-tower again. Let $A_n$ be the minimum number of moves, hence $A_n=2A_{n-1}+2=2^{n+1}-2$.
1.11b
Let $\require{enclose}\enclose{horizontalstrike}{B_n}$ be the minimum number of moves to move a double $\require{enclose}\enclose{horizontalstrike}{n}$-tower in the original order; $\require{enclose}\enclose{horizontalstrike}{H_n}$ be the minimum number of moves to move a double $\require{enclose}\enclose{horizontalstrike}{n}$-tower except for the bottom disk. Then we have $\require{enclose}\enclose{horizontalstrike}{B_n=H_n+1+B_{n-1}+1+B_{n-1}}$ and $\require{enclose}\enclose{horizontalstrike}{H_n=B_{n-1}+1+B_{n-1}}$.
Insert $\require{enclose}\enclose{horizontalstrike}{H_n}$ to the $\require{enclose}\enclose{horizontalstrike}{B_n}$ equation, we could get $\require{enclose}\enclose{horizontalstrike}{B_n=4B_{n-1}+3=4^n-1}$.
By referring to the answer, I found out that my approach above wasn’t correct. I’ve made a mistake that I postulated all disks never change the order during their moves, which is not necessary.
It can be shown that no strategy does better than $B_n=A_{n-1}+2+A_{n-1}+2+B_{n-1}$. This strategy changes the order of bottom two disks twice but doesn’t care whether the upper disks keep the order during their moves, which is also the reason why we use $A_n$ here. Thus, $B_n=2^{n+2}-5$.
1.12
$$A(m_1,\ldots,m_n)=2A(m_1,\ldots,m_{n-1})+m_n.$$
This is an equation of the “generalized Josephus” type, whose solution is $(m_1\ldots m_k)_2$.
1.13
We already know $n$ straight lines define $L_n=\frac{n(n+1)}2+1$ regions on a plane, and when the $n$-th line is added in, $n$ new areas are created.
Let the zig-zags be extremely narrow to be seen as straight lines to some extent. So when the $n$-th zig-zag is added in, $n$ new areas are created “in the straight line manner.”
We could also see that when two zig-zags intersect, $8$ new areas are created “around their intersection” in the way shown below:
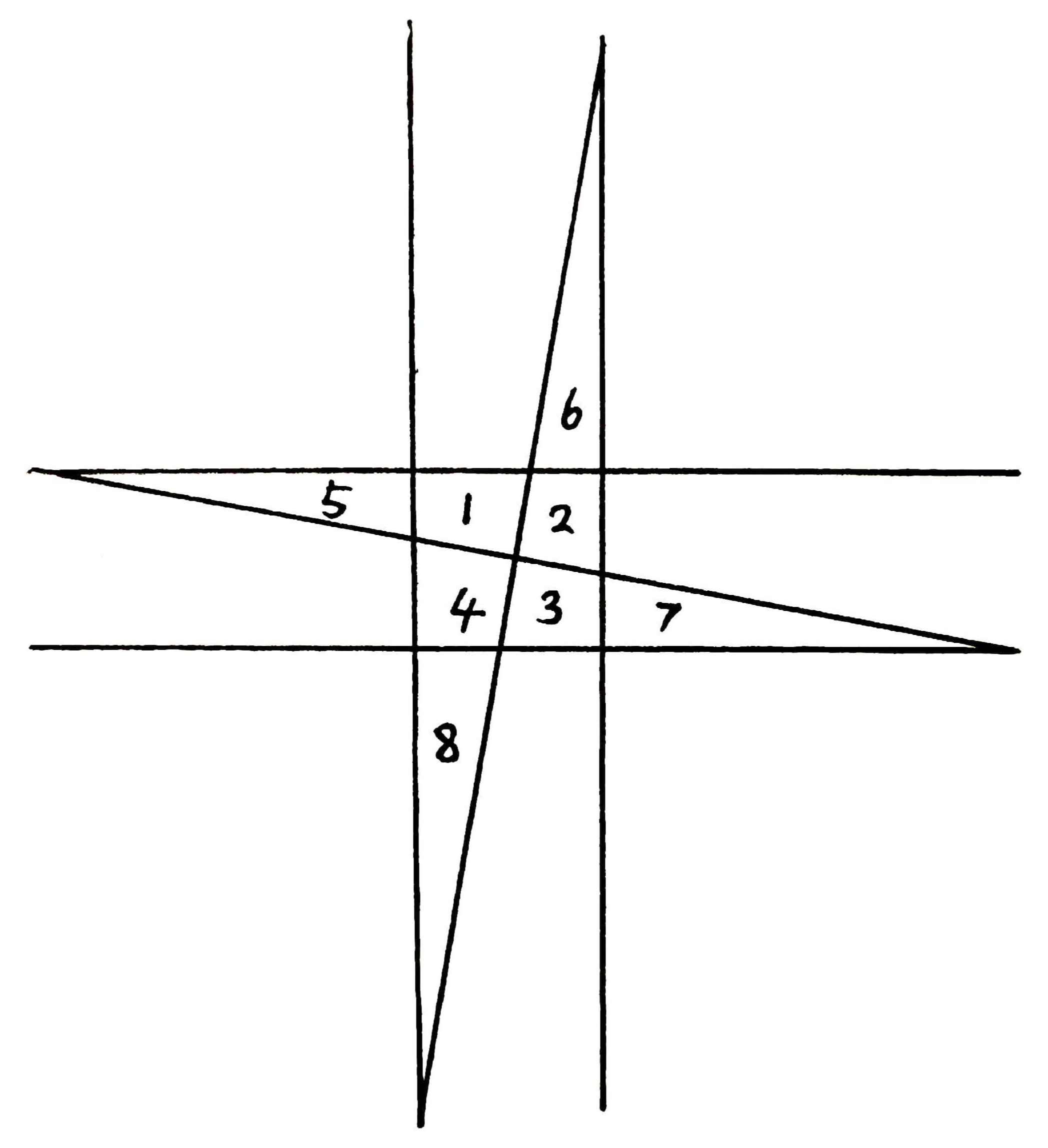
And when the $n$-th zig-zag is added in, there are at most $n-1$ new “intersections.” So
$$Z\!Z_n=Z\!Z_{n-1}+n+8(n-1)=\frac92n^2+\frac72n+1.$$
1.14
$n$ new areas are created when the $n$-th line is added into the plane, which is equal to the maximum number of line segments created by splitting a line with $n-1$ points. Analogously, $L_{n-1}$ new pieces of cheese is created when making the $n$-th slice.
So, in recurrence form
$$P_n=\begin{cases}1,&\text{if $n=0$};\\P_{n-1}+L_{n-1},&\text{if $n>0$}.\end{cases}$$
We have $P_5=26$.
1.15
The function $I$ has the same recursion relation as $J$, but with different boundary values, which are $I(2)=2,I(3)=1$.
Thus, we cannot find a unique $I(1)$ that satisfies this recurrence. So we have to split it into two cases, one with $I(2)=2$ and one with $I(3)=1$.
Let’s represent in terms of $n=2^m+l$, and let $\beta_0=-1,\beta_1=1$. The recurrence unfolds, binary-wise:
$$\begin{aligned}I\big((b_mb_{m-1}\ldots b_0)_ 2\big)&=2I\big((b_mb_{m-1}\ldots b_1)_ 2\big)+\beta _ {b_0}\\&\;\;\vdots\\&=2^{m-1}I\big((b_mb_{m-1})_2\big)+\cdots+2\beta _{b_1}+\beta _{b_0}.\end{aligned}$$
Then we can stop here, so far the function $I$ have the same form as $J$, and the two leading bits $(b_mb_{m-1})_2$ are enough to contain the two cases:
$$\begin{aligned}J(2)=1,I(2)=2&\implies I(n)-J(n)=2^{m-1};\\J(3)=3,I(3)=1&\implies I(n)-J(n)=-2^m.\end{aligned}$$
That is to say
$$I(n)=\begin{cases}J(n)+2^{m-1},&\text{if $0\leq l<2^{m-1}$};\\J(n)-2^m,&\text{if $2^{m-1}\leq l<2^m$}.\end{cases}$$
1.16
Express $g(n)$ in the form
$$g(n)=A(n)\alpha+B(n)\beta_0+C(n)\beta_1+D(n)\gamma.$$
Let $g(n)=1$, which implies $(\alpha,\beta_0,\beta_1,\gamma)=(1,-2,-2,0)$. Then
$$A(n)-2B(n)-2C(n)=1.\tag{1}$$
Let $g(n)=n$, which implies $(\alpha,\beta_0,\beta_1,\gamma)=(1,0,1,-1)$. Then
$$A(n)+C(n)-D(n)=n.\tag{2}$$
Let $(\alpha,\beta_0,\beta_1,\gamma)=(1,-2,-2,0)$, which gives $g(n)=3^m$. Then (note we’re representing in terms of $n=2^m+l$)
$$A(n)=3^m.\tag{3}$$
Let $(\alpha,\beta_0,\beta_1,\gamma)=(0,0,1,0)$. Similar to the binary expansion in the Josephus problem, we have
$$C(n)=(b_{m-1}\ldots b_0)_3.\tag{4}$$
I also checked that for $(1)(2)(3)$ and $(4)$,
$$\left|\begin{array}{cccc}1&-2&-2&0\\1&0&1&-1\\1&0&0&0\\0&0&1&0\end{array}\right|\neq0.$$
The recurrence is solvable; hence
$$\begin{aligned}A(n)&=3^m;\\B(n)&=\big(3^m-2(b_{m-1}\ldots b_0)_ 3-1\big)/2;\\C(n)&=(b_{m-1}\ldots b_0)_ 3;\\D(n)&=3^m+(b_{m-1}\ldots b_0)_3-n.\end{aligned}$$
Then
$$\begin{aligned}g(n)&=3^m\alpha+\big(3^m-2(b_{m-1}\ldots b_0)_ 3-1\big)\frac{\beta_0}2+(b_{m-1}\ldots b_0)_ 3\beta_1+\big(3^m+(b_{m-1}\ldots b_0)_ 3-n\big)\gamma\\&=\left(\alpha+\frac{\beta_0}2+\gamma\right)3^m+(-\beta_0+\beta_1+\gamma)(b_{m-1}\ldots b_0)_3-\frac{\beta_0}2-n\gamma.\end{aligned}$$