February 15, 2020 duinomaker

2020牛客寒假算法基础集训营6

解题报告 ( ABCDEFGHIJ )

2020-02-18 增加H题题解

比赛链接：2020牛客寒假算法基础集训营6

A. 配对

题目描述

现在有正整数集合 $A$ 和 $B$，每个集合里有 $N$ 个数，你要建立他们间的一一映射
将每对配对的数字相加可以得到 $N$ 个和，你要做的就是最大化第 $K$ 大的和
$1\leq K\leq N\leq100,000$ 输入的所有数字不超过 $10^8$

输入描述

第一行 $2$ 个数字 $N,K$
接下来两行，每行 $N$ 个正整数，分别表示 $A$ 和 $B$ 中的元素

输出描述

一行，表示第 $K$ 大的和的最大值

示例

输入

1
2
3

3 2
1 2 3
1 2 3

输出

题解

为了使相加后第 $K$ 大的数最大，应该将 $A$ 序列前 $K$ 大的数，与 $B$ 序列前 $K$ 大的数相配对。

如此看来，可以只保留 $A$ 序列和 $B$ 序列前 $K$ 大的项，而直接舍弃所有后面的项。此时题目便转化为了：将 $A$ 序列和 $B$ 序列前 $K$ 大的项配对求和，求和后序列的最小值最大是多少？

为了使最小值尽量大，可以将 $A$ 序列由大到小排序，$B$ 序列由小到大排序，并逐项相加。最后求出序列的最小值，就是答案。

参考代码

A.cpp

#include <bits/stdc++.h>
#define rep(i, l, r) for (int i = l, i##_ = r; i < i##_; ++i)
using namespace std;
constexpr int MAX_N = 1e5 + 7;

int A[MAX_N], B[MAX_N];

int main()
{
    int n, k;
    scanf("%d%d", &n, &k);
    rep(i, 0, n) scanf("%d", &A[i]);
    rep(i, 0, n) scanf("%d", &B[i]);
    sort(A, A + n, greater<int>());
    sort(B, B + n);
    for (int i = 0; i != k; ++i)
        A[i] += B[i + n - k];
    int ans = A[0];
    rep(i, 1, k)
        if (A[i] < ans)
            ans = A[i];
    printf("%d\n", ans);
}

B. 图

题目描述

现在有一个 $N$ 个点的有向图，每个点仅有一条出边（有可能出现自环）
你需要求出图中最长的简单路径包含点的数量
$(1\leq N\leq1,000,000)$

输入描述

第一行，一个数字 $N$
接下来 $N$ 行，每行一个正整数，第 $i+1$ 行的数字表示第 $i$ 个点出边终点的编号
（点从 $1$ 开始标号）

输出描述

一行一个数字，最长的简单路径的长度

示例

输入

输出

题解

简单路径即不重复经过同一点的路径，这题考察了深度优先搜索技巧。记录下某一点所指向的点 $(to_i)$，该点是否已被访问过 $(vis_i)$，以及以该点为起点最多经过多少点 $(len_i)$ 。

具体实现方法见代码。

参考代码

B.cpp

#include <bits/stdc++.h>
using namespace std;

constexpr int MAXN = 1e6 + 7;

bool vis[MAXN];
int len[MAXN], to[MAXN];
int ans;

void dfs(int x)
{
    vis[x] = true;
    if (vis[to[x]]) {
        if (len[to[x]]) {
            len[x] = len[to[x]] + 1;
        } else {
            int curr = to[x], cnt = 1;
            while (curr != x) {
                ++cnt;
                curr = to[curr];
            }
            curr = to[x];
            while (curr != x) {
                len[curr] = cnt;
                curr = to[curr];
            }
            len[x] = cnt;
        }
    } else {
        dfs(to[x]);
        if (!len[x])
            len[x] = len[to[x]] + 1;
    }
    if (len[x] > ans)
        ans = len[x];
}

int main()
{
    int n;
    scanf("%d", &n);
    for (int i = 1; i <= n; ++i)
        scanf("%d", &to[i]);
    for (int i = 1; i <= n; ++i)
        if (!vis[i])
            dfs(i);
    printf("%d\n", ans);
}

C. 汉诺塔

题目描述

现在你有 $N$ 块矩形木板，第 $i$ 块木板的尺寸是 $X_i\times Y_i$，你想用这些木板来玩汉诺塔的游戏。
我们知道玩汉诺塔游戏需要把若干木板按照上小下大的顺序堆叠在一起，但因为木板是矩形，所以有一个问题：
第 $i$ 块木板能放在第 $j$ 块木板上方当且仅当 $X_i < X_j$ 且 $Y_i < Y_j$，于是你很可能没法把所有的木板按照一定的次序叠放起来。
你想把这些木板分为尽可能少的组，使得每组内的木板都能按照一定的次序叠放。
你需要给出任意一种合理的分组方案。
提醒：“任意” 意味着你的答案不必和标准输出完全一致，只要正确即可。

输入描述

第一行，一个正整数 $N$
接下来 $N$ 行，每行两个正整数表示 $X_i$ 和 $Y_i$
对于所有的数据 $1\leq N\leq100,000$ 且 $1\leq X_i,Y_i\leq N$，$X_i$ 互不相等且 $Y_i$ 互不相等

输出描述

输出文件包含两行，第一行一个正整数，表示最少组数
第二行 $N$ 个正整数，依次表示你的方案中每块木板分在了哪一组
组的编号必须是从 $1$ 开始的连续整数

示例

输入

输出

1
2

2
1 1 2

题解

待补充

参考代码

C.cpp

D. 重排列

题目描述

一个序列的重排列是指对这个序列中的元素进行若干次（包括 $0$ 次）交换操作后得到的新序列
在本题中，序列中可能出现重复的数字，他们被视作不同的元素
例如，序列 $1\quad1$ 的重排列有两种
现在有两个长度为 $N$ 的非负整数序列 $A$ 和 $B$，问有多少种 $A$ 的重排列满足对于所有的 $1\leq i\leq N$，有 $A_i\leq B_i$
由于答案可能很大，你只需要输出答案对 $10^9+7$ 取模的结果

输入描述

输入第一行，包含一个正整数 $N$
接下来一行，$N$ 个非负整数表示序列 $A$
再接下来一行，$N$ 个非负整数表示序列 $B$
$1\leq N\leq100,000$ 且 $0\leq A_i,B_i\leq10^9$

输出描述

一行一个整数，表示答案

示例

输入

1
2
3

4
1 1 2 3
1 2 3 4

输出

题解

首先将 $A$ 序列和 $B$ 序列分别由小到大排序。对于 $B$ 序列的每一项，$A$ 序列中小于这一项的项数可以求出，这项数代表可选的排列方案数。

还要注意的是，已选择的数不能重复选择，需要从方案数里减去已选数的个数。最后将这些方案数相乘即可得出答案：

$$Answer =\prod_{i=1}^{N}(A\,\text{序列中不大于}\,B_i\,\text{的项数} - (i-1))$$

参考代码

D.cpp

#include <bits/stdc++.h>
#define rep(i, l, r) for (int i = l, i##_ = r; i < i##_; ++i)
using namespace std;
using ll = long long;

constexpr ll MAXN = 1e5 + 7;
constexpr ll MOD = 1e9 + 7;

ll A[MAXN], B[MAXN];

int main()
{
    int n;
    ll ans = 1;
    scanf("%d", &n);
    rep(i, 0, n) scanf("%lld", &A[i]);
    rep(i, 0, n) scanf("%lld", &B[i]);
    sort(A, A + n);
    sort(B, B + n);
    rep(i, 0, n)
        ans = (ans * (upper_bound(A, A + n, B[i]) - A - i)) % MOD;
    printf("%lld\n", ans);
}

E. 立方数

题目描述

对于给定的正整数 $N$，求最大的正整数 $A$，使得存在正整数 $B$，满足 $A^3B=N$
输入包含 $T$ 组数据，$1\leq T\leq10,000$ 且 $1\leq N\leq10^{18}$

输入描述

第一行数字 $T$ 表示数据组数
接下来一行，$T$ 个正整数 $N$

输出描述

$T$ 行，每行一个数字表示答案

示例

输入

1 2	4 27 24 7 54

输出

题解

待补充

参考代码

E.cpp

F. 十字阵列

题目描述

小Q 新学会了一种魔法，可以对一个 $N$ 行 $M$ 列的网格上的敌人造成伤害
第 $i$ 次使用魔法可以对网格上的一个十字形区域（即第 $x_i$ 行和第 $y_i$ 列的合并）中的每个格子上的敌人造成 $z_i$ 点伤害
现在小Q 一共使用了 $H$ 次魔法，你需要在所有的施法完成之后统计造成伤害的情况，详见输出描述
提醒：本题输入规模较大，请使用高效的输入方式
$1\leq H\leq500,000$ 且 $1\leq x_i,y_i,z_i,N,M\leq2000$ 且 $1\leq x_i\leq N$ 且 $1\leq y_i\leq M$

输入描述

第一行 $3$ 个数字 $N,M,H$
接下来 $H$ 行，每行 $3$ 个正整数 $x_i，y_i，z_i$

输出描述

为了避免大量的输出，假设第 $i$ 行第 $j$ 列受到的总伤害是 $w_{ij}$
你只需要输出 $\sum{(w_{ij}\times(i+j))}$ 对 $10^9+7$ 取模的结果即可

示例

输入

输出

题解

加权求和。每个方块的权值是已知的 $(i+j)$，一个点对总伤害的贡献，等于该行和该列所有权值的和，乘以伤害。

参考代码

F.cpp

#include <bits/stdc++.h>
#define rep(i, l, r) for (ll i = l, i##_ = r; i < i##_; ++i)
using namespace std;
using ll = long long;

constexpr ll MOD = 1e9 + 7;

void read(ll&a, ll&b, ll&c)
{
    char ch;
    a = b = c = 0;
    while ((ch = getchar()) >= '0' && ch <= '9')
        a = (a << 3) + (a << 1) + (ch & 0xf);
    while ((ch = getchar()) >= '0' && ch <= '9')
        b = (b << 3) + (b << 1) + (ch & 0xf);
    while ((ch = getchar()) >= '0' && ch <= '9')
        c = (c << 3) + (c << 1) + (ch & 0xf);
}

int main()
{
    ll n, m, h, x, y, z;
    read(n, m, h);
    ll ans = 0, mn = ((m + 1) * m + (n + 1) * n) >> 1;
    rep(i, 0, h) {
        read(x, y, z);
        ans = (ans + (mn + x * m + y * n - x - y) * z) % MOD;
    }
    printf("%lld\n", ans);
}

G. 括号序列

题目描述

合法括号序列的定义是：

空序列是合法括号序列
如果 $S$ 是一个合法括号序列,那么 $(S)$ 是合法括号序列
如果 $A$ 和 $B$ 都是合法括号序列,那么 $AB$ 是一个合法括号序列

现在给定一个括号序列，求最少删去几个括号能得到一个合法的括号序列
输入包含 $T$ 组数据，每组数据中，设括号序列的长度为 $N$
$1\leq T,\sum^T{(N)}\leq1,000,000$
（由于空串是合法的括号序列，所以答案可以是 $N$）

输入描述

第一行一个数字 $T$
接下来 $T$ 组数据共 $2T$ 行，每组数据第一行是 $N$
第二行则是一个长度为 $N$ 的括号序列

输出描述

$T$ 行 $T$ 个数字，表示输入的括号序列最少删去几个括号能得到一个合法的括号序列

示例

输入

2
6
())(()
9
()(()()))

输出

1
2

2
1

题解

记录未封闭的左括号数量。若没有未封闭括号却又出现了右括号，删去；若读取到末尾仍有未封闭括号，说明之前有相同数量的左括号需要删去。

参考代码

G.cpp

#include <bits/stdc++.h>

int main()
{
    int T;
    scanf("%d", &T);
    while (T--) {
        int n, cnt = 0, ans = 0;
        scanf("%d ", &n);
        for (int i = 0; i != n; ++i) {
            if (getchar() == '(') {
                ++cnt;
            } else {
                if (cnt)
                    --cnt;
                else
                    ++ans;
            }
        }
        printf("%d\n", ans + cnt);
    }
}

H. 云

题目描述

现在天空（可视为二维平面）中有 $N$ 朵 ${\rm A}$ 类云，$M$ 朵 ${\rm B}$ 类云，每朵云的形状都可以用边平行于坐标轴的矩形来描述。
一开始，${\rm A}$ 类云在第三象限，${\rm B}$ 类云在第一象限，没有任何云和坐标轴有交点。
随着风的吹拂，${\rm A}$ 类云以每秒一个单位的速度向右移动，${\rm B}$ 类云以每秒一个单位的速度向下移动，当一朵 ${\rm A}$ 类云和一朵 ${\rm B}$ 类云在某一个时刻有了至少一个公共点，它们就相遇了。
现在请你告诉小R，有多少对 ${\rm A}$ 类云和 ${\rm B}$ 类云能够相遇。
$1\leq N,M\leq100,000$ 且 $1\leq|X_i|,|Y_i|,|P_i|,|Q_i|\leq10^9$

注：

本题输入规模较大，请注意输入的效率
输入的云的形状可能为退化的矩形（直线或点）

输入描述

输入第一行，包含两个正整数 $N$ 和 $M$
接下来 $N$ 行，每行描述一朵 ${\rm A}$ 类云
再接下来 $M$ 行，每行描述一朵 ${\rm B}$ 类云
一朵云的位置用一行四个数 $A_i,B_i,C_i,D_i$ 表示，意为这朵云左上角在 $(A_i,B_i)$，右下角在 $(C_i,D_i)$

输出描述

一行一个整数，表示答案

示例

输入

1
2
3

1 1
-2 -1 -1 -2
1 2 2 1

输出

题解

这题需要换个角度思考：${\rm A}$ 类云向右运动，${\rm B}$ 类云向下运动。只是粗略想想的话，会觉得是个很复杂的运动。

但如果我们在坐标系中添加这样一条辅助线 $(x+y=0)$呢？

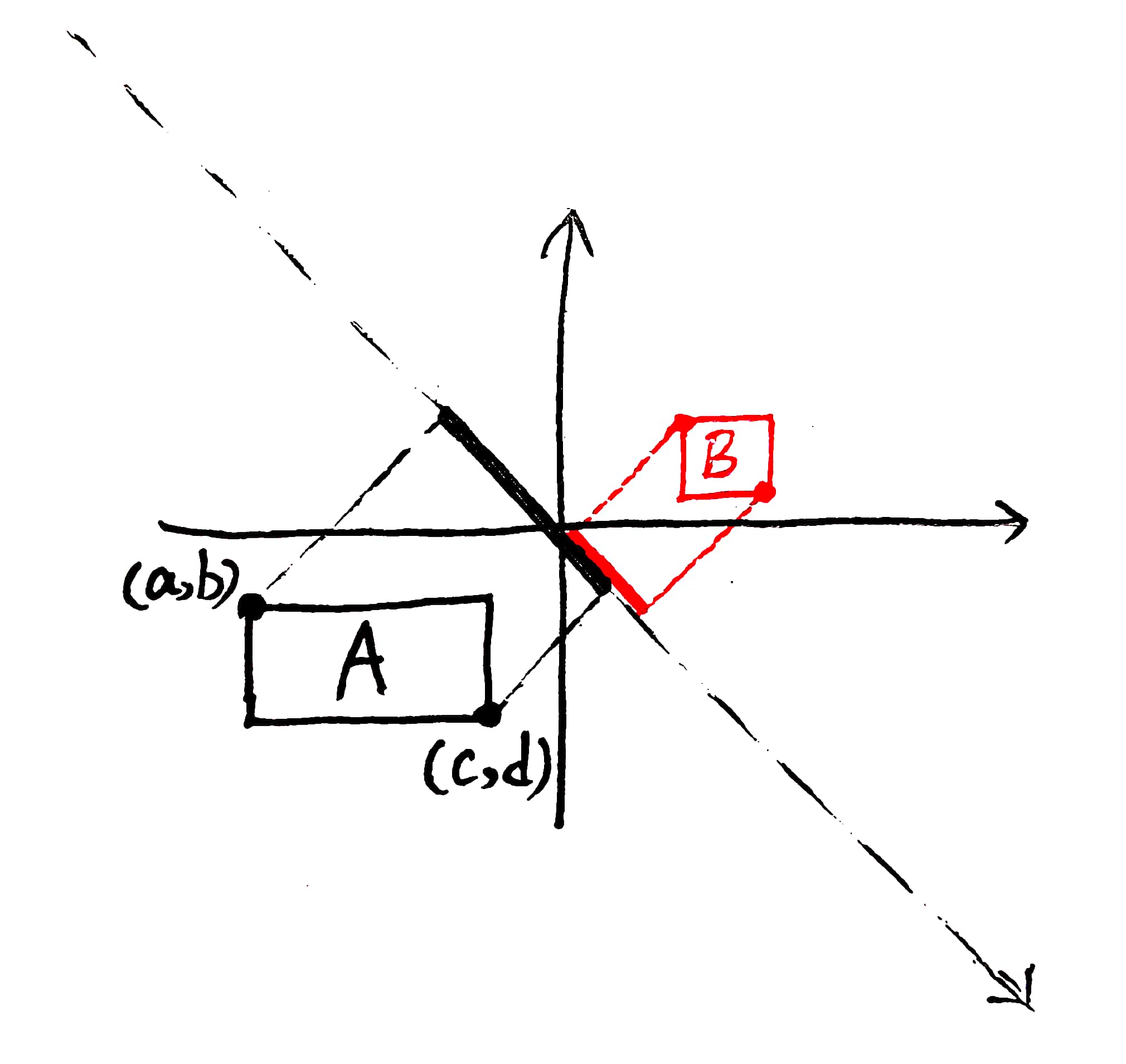
如图所示，上述运动便可描述为 “云朵们面对辅助线，向对面的云靠近，并同时向右下角移动”。

我们甚至可以忽略 “并同时向右下角移动”，因为这样并不会影响云彩相遇与否。

如此一来，若两朵云会相遇，它们一定会在辅助线上扫过一个共同的区域。例如，图中红色线段与黑色线段有重合部分，它们一定会相遇。

所以可以采用投影的方法，将云彩投影到辅助线上，得到一条线段，其在辅助线上的覆盖范围是 $[a-b,c-d]$ 。最后清点有重合部分的线段对数，即可得到答案。

清点前需记录下覆盖范围的端点 $(node)$，包括其坐标 $(pos)$ 、左端点还是右端点 $(lr)$ 、${\rm A}$ 类云还是 ${\rm B}$ 类云 $(type)$ 。

具体实现见参考代码，参考了牛客上某些大神的已通过代码，一开始看得很懵，不过领悟了这投影的方法就很好理解了。

参考代码

H.cpp

#include <bits/stdc++.h>
using namespace std;

constexpr int MAXN = 4e5 + 7;

struct node {
    int pos;
    int lr;
    int type;

    bool operator<(const node& rhs) const
    {
        if (pos == rhs.pos)
            return lr > rhs.lr;
        return pos < rhs.pos;
    }
} nodes[MAXN];

int main()
{
    int n, m, k = 0;
    int a, b, c, d;
    long long cnt[2] = {}, ans = 0;

    scanf("%d%d", &n, &m);
    while (n--) {
        scanf("%d%d%d%d", &a, &b, &c, &d);
        nodes[k++] = { a - b, 1, 0 };
        nodes[k++] = { c - d, -1, 0 };
    }
    while (m--) {
        scanf("%d%d%d%d", &a, &b, &c, &d);
        nodes[k++] = { a - b, 1, 1 };
        nodes[k++] = { c - d, -1, 1 };
    }
    sort(nodes, nodes + k);

    for (int i = 0; i != k; ++i) {
        cnt[nodes[i].type] += nodes[i].lr;
        if (nodes[i].lr == 1)
            ans += cnt[nodes[i].type ^ 1];
    }
    printf("%lld\n", ans);
}

I. 导航系统

题目描述

小Q 所在的国家有 $N$ 个城市，城市间由 $N-1$ 条双向道路连接，任意一对城市都是互通的。
每条道路有一个长度，自然，小Q 的导航系统能显示每对城市间的最短距离。
但是小Q 对这个系统并不太放心，于是他向你求助：
给定每对城市间的最短距离，你要判断距离表是否一定有误。
如果这张距离表是自洽的，那么请你按升序依次给出每条道路的长度。
对于全部的数据，$1\leq N\leq500$，输入的所有数字都是不超过 $10^9$ 的非负整数。

输入描述

第一行一个数字 $N$
接下来 $N$ 行，每行 $N$ 个正整数
第 $i$ 行第 $j$ 列的数字表示城市 $i$ 和城市 $j$ 间的最短距离
保证第 $i$ 行第 $i$ 列的数字为 $0$

输出描述

第一行，一个字符串
如果距离表没有问题，输出 Yes
并在接下来的 $N-1$ 行从小到大给出每条道路的长度
否则输出 No 即可

示例1

输入

输出

1
2
3

Yes
1
1

示例2

输入

输出

No

题解

待补充

参考代码

I.cpp

J. 签到题

题目描述

现有一个边长为正整数的三角形，问能否以其三个顶点为圆心画三个圆，使三个圆两两外切
三边长均不超过 $10^8$

输入描述

三个正整数，表示三角形的边长

输出描述

如果三条边不能构成三角形，输出 wtnl
如果三条边能构成三角形但不能画出符合要求的圆，输出 No
否则输出一行 Yes
然后在第二行输出一组方案，按升序给出三个圆的半径，保留两位小数

示例

输入

2 3 3

输出

1 2	Yes 1.00 1.00 2.00

题解

初中数学？

参考代码

J.cpp

#include <bits/stdc++.h>
using namespace std;
using ll = long long;

int main()
{
    ll a, b, c;
    scanf("%lld%lld%lld", &a, &b, &c);
    if (a > b) swap(a, b);
    if (b > c) swap(b, c);
    if (a > b) swap(a, b);
    if (a + b <= c) puts("wtnl"), exit(0);
    printf("Yes\n%.2f %.2f %.2f\n", (double)(b + a - c) / 2.0,
                                    (double)(a + c - b) / 2.0,
                                    (double)(b + c - a) / 2.0);
}

#Depth-first Searching#Graph Theory