线段树之基本概念
本文介绍了线段树的基础知识,辅之以相关例题。
基本概念部分,因为是初学,理解没有那么深入,自己总结出来可能质量不高,所以本文的前半部分基本照搬了 $\text{SilentEAG}$ 大佬的 这篇文章(有修改),自己着重写了习题部分。
什么是线段树?
首先,你得有树的基本知识。
然后。
线段树是一种二叉搜索树,与区间树相似,它将一个区间划分成一些单元区间,每个单元区间对应线段树的一个结点。
很懵?没关系,我们继续。
其实,线段树(Segment Tree)是一种基于分治思想的二叉树结构,如果你学过树状数组,你会清楚地知道两者的差异性,并且随着学习的深入,你会发现线段树是一种更为通用的数据结构。
可以说,只要是能满足区间可加性(也就是大区间的信息能由它的两个子区间整理得到)的操作,大都可以用线段树解决。
最基本的线段树包含以下几个概念:
- 线段树每个节点表示一个区间;
- 线段树的唯一根节点表示整个区间统计范围,如 $[1,N]$ ;
- 线段树的每个叶节点表示一个长度为 $1$ 的元区间,如 $[x,x]$ ;
- 线段树上的每个节点 $[l,r]$,它的左子节点是 $[l,mid]$,右子节点是 $[mid+1,r]$,其中 $mid=(l+r)/2$ (这是线段树最常见的写法,也会有适用于不同问题的其它写法,不过这用于理解线段树的要义足矣)。
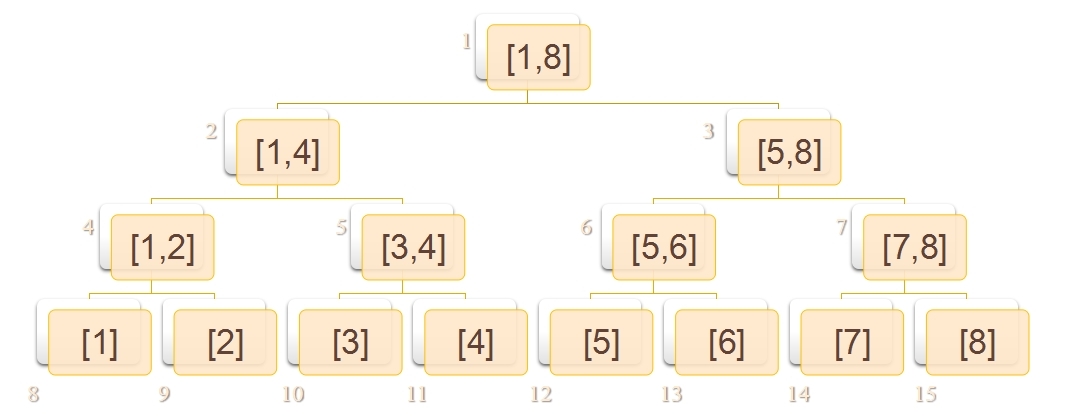
如图,这就是一棵线段树。我们可以发现,当整个区间统计长度为 $2$ 的整数次幂时,整棵线段树一定是一棵完全二叉树,那我们就可以用堆的编号方法来给线段树来编号啊(其实图中已经编好了)。
如果根节点编号为 $1$ 。编号为 $x$ 的节点,它的左儿子编号为 $2x$,右儿子编号为 $2x+1$ 。
这样,我们就可以用一个数组来存所有节点的编号了!
诶等等,那万一整个区间长度不是 $2$ 的整数次幂呢?
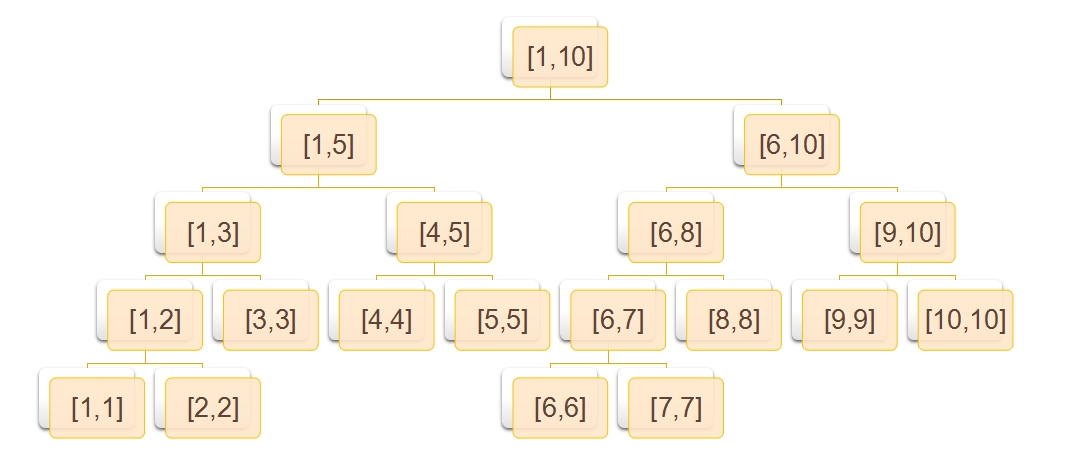
可以惊讶地发现,我们同样可以使用 “父子二倍标记法”。正确性显然,只不过,正是因为这种情况,所以树的最后一层节点编号在数组中的位置可能不是连续的。
如果区间长度为 $N$,在最理想的状况下,即 $N$ 是 $2$ 的整数次幂时,$N$ 个叶节点的满二叉树有 $N+N/2+N/4+\ldots+1=2N−1$ 个节点。只要不是这种情况,那就还有一层,所以我们保存线段树节点编号的数组的长度 $T$ 要足够。实际应用时将 $N$ 补至 $2$ 的整数次幂,再乘以 $2$ 即可,实际使用时就是这样:
$$\begin{aligned}N=10^4\to T=2^{15}\\N=10^5\to T=2^{18}\\N=10^6\to T=2^{21}\end{aligned}$$
当然,不想麻烦的话,可以直接 $T=4N$,也没有问题。
于是线段树信息储存如下:
1 | struct node { |
当然,线段树的写法多种多样,这是最稳的一种,还有一种是记录左右儿子编号的,据说叫做zkw线段树,我以后遇到了可能会补充。
建树
我们需要从根节点 “$1$” 出发,向下递归建树,并把每个节点所代表的区间赋给它。当到达了根节点,便传值,再向上维护信息。
以维护区间和为例,我们可以这样建树:
1 | void build(int l, int r, int p = 1) |
单点修改
显然,每次操作,我们都需要从根节点开始遍历,递归找到需要修改的叶子节点,然后修改,然后向上传递信息。
1 | void modify(int x, int val, int p = 1) |
因为整棵树的深度是 $\lceil\log N\rceil$,所以单次修改的时间复杂度为 $O(\log N)$ 。
区间查询
这里直接给出算法过程,正确性显然。
- 若当前节点所表示的区间已经被询问区间所完全覆盖,则立即回溯,并传回该点的信息;
- 若当前节点的左儿子所表示的区间已经被询问区间所完全覆盖,就递归访问它的左儿子;
- 若当前节点的右儿子所表示的区间已经被询问区间所完全覆盖,就递归访问它的右儿子。
以返回区间和为例:
1 | int query(int x, int y, int p = 1) |
为什么使用线段树?
先来对比一下普通数组和线段树,看看它们各种操作的时间复杂度。
| | 初始化 | 区间查询 | 单节点修改 |
|---|---|---|---|
| 普通数组 | $O(n)$ | $O(n)$ | $O(1)$ |
| 线段树 | $O(n)$ | $O(\log n)$ | $O(\log n)$ |
可见,线段树主要是在区间查询上有速度优势,能够应对更多、范围更大的查询。但是相应地,单节点修改需要耗费很多时间。
然而,线段树很懒,懒得一个个地处理节点修改的请求。为了应对需要修改多个节点的情况,线段树有它自己的策略——“懒惰标记”,接下来会学到。
不过在这之前,先做几道练习题。
【习题】Can you answer these queries III
需要你提供一种数据结构使之能够查询区间最大连续子段和,并且支持单点修改。
题解
首先考虑区间的最大子段的这些情况:
- 连续最大和的区间只在左儿子所对应的区间上;
- 连续最大和的区间只在右儿子所对应的区间上;
- 连续最大和的区间横跨左右儿子的区间。
第 $1$ 和第 $2$ 种情况,答案就是左边部分(右边部分)的最大子段和。
第 $3$ 种情况复杂一点,答案等于 左边部分从其右端开始的最大子段和 加上 右边部分从其左端开始的最大子段和。
当然,为了维护区间从其端点开始的最大子段和,还需维护区间和 $(sum)$ 。如此,一个区间从其左端开始的最大子段和,假设左右儿子的位置分别为 $chl$ 和 $chr$,便可以如此维护:
$$prel_p =\max\{prel_{chl} , sum_{chl} + prel_{chr}\}$$
从右端开始的最大子段和同理。
总的来说,我们要维护这几种区间信息:
- 区间的最大连续子段和 $(val)$
- 区间和 $(sum)$
- 区间从其左端开始的最大子段和 $(prel)$
- 区间从其左端开始的最大子段和 $(prer)$
接下来是查询部分,一开始当然是在根节点查询所给的区间。在每个节点处的查询又可以分为三种情况处理:
- 所查询的区间刚好是该节点的区间,则直接返回该区间;
- 所查询的区间全部在该节点区间的左半部分,则返回该节点左儿子查询该区间的结果;
- 所查询的区间全部在该节点区间的右半部分,则返回该节点右儿子查询该区间的结果;
- 所查询的区间横跨该节点区间的中间,则将所查询的区间根据该节点区间的中点分为左右两部分,分别让该节点的左儿子和右儿子查询这两个区间,并将查询结果 “合并” 后返回。
所谓 “合并” 的操作其实就是建树时,子节点向上传播信息的操作,我们可以复用这段代码,也就是下方参考代码中的 pushup 函数。
参考代码
1 |
|
【习题】Crane
有一台起重机。起重机可以看成由 $N$ 条线段首尾相接而成。第 $i$ 条线段的长度是 $L_i$ 。
最开始,所有的线段都笔直连接,指向上方。
有 $C$ 条操纵起重机的指令。指令 $i$ 给出两个整数 $S_i$ 和 $A_i$,效果是使线段 $S_i$ 和 $S_{i+1}$ 之间的角度变成 $A_i$ 度。其中角度指的是从线段 $S_i$ 开始沿逆时针方向旋转到 $S_{i+1}$ 所经过的角度。最开始所有的角度都是 $180$ 度。
按顺序执行这 $C$ 条指令,在每条执行后,输出起重机末端(第 $N$ 条线段的端点)的坐标。假设起重机支点的坐标是 $(0,0)$ 。
题解
这是在白书上看到的题目,思维难度比较高。花了两天时间才搞懂,我还是太菜了。思路是运用分治的思想,将整个起重机逐次二分为小区间,用线段树解决。每个节点代表一段连续的线段的集合,并维护这两个值:
- 将节点左子节点的向量所指的方向作为竖直向上的正方向后,从该节点左子节点的向量起点指向该节点右子节点的向量终点的向量;
- 将节点的左右子节点的向量拼接后,右子节点的向量需要旋转的角度。
第一个值容易维护,如果节点 $p$ 表示的向量是 $(x_p,y_p)$,角度是 $ang_p$,两个儿子节点分别是 $chl$ 和 $chr$,则有:
$$\begin{aligned}x_p=x_{chl}+(\cos(ang_p)\times x_{chr}-\sin(ang_p)\times y_{chr})\\y_p=y_{chl}+(\sin(ang_p)\times x_{chr}+\cos(ang_p)\times y_{chr})\end{aligned}$$
比较难维护的是第二个值,旋转角度。我随手画了个图方便理解。
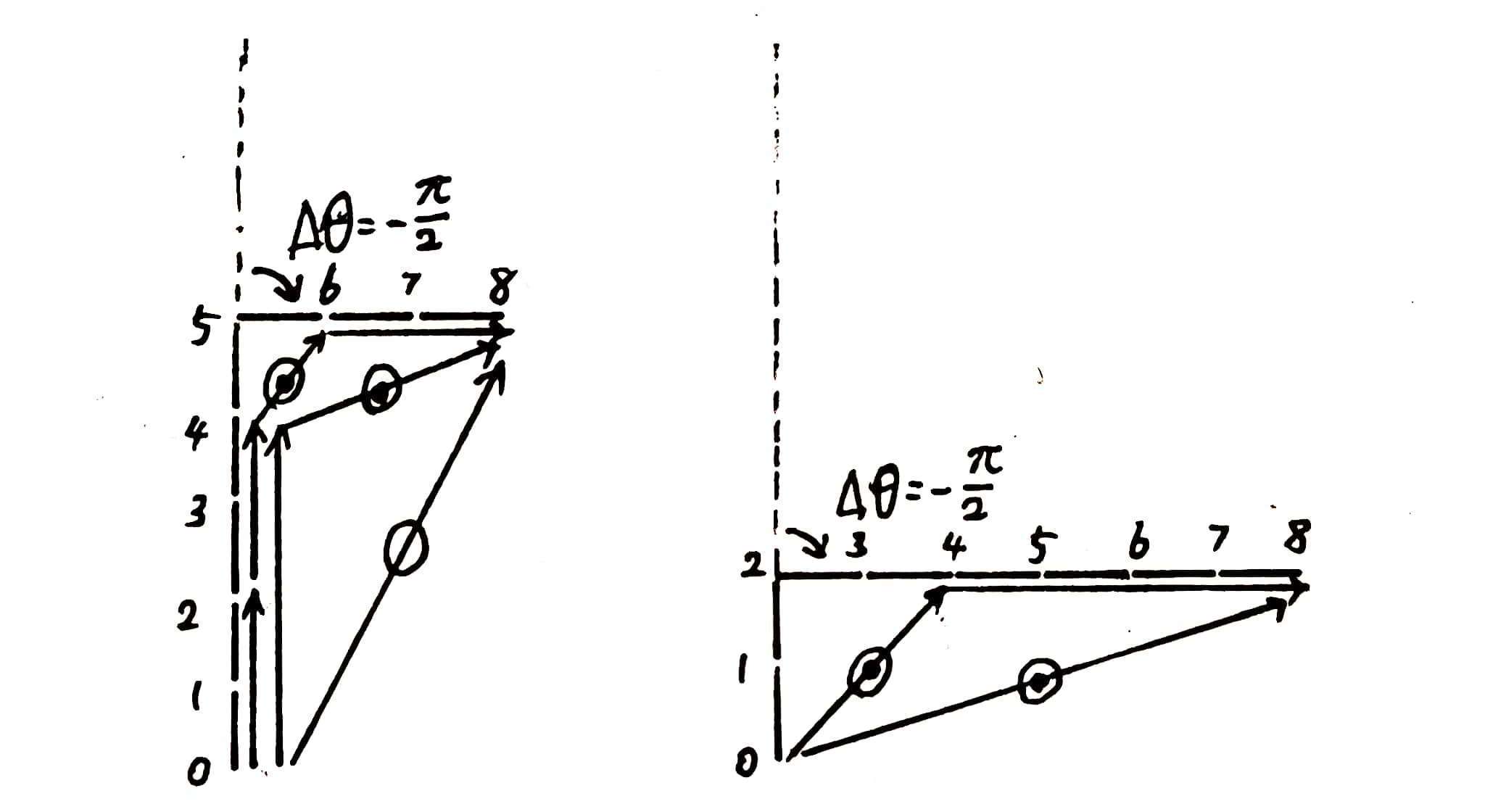
这张图是 $N=8$ 时的两种情况,左图是将第 $5$ 节变为 $90$ 度,右图是将 $2$ 节变为 $90$ 度。每个带方向的箭头都是某个节点所对应的向量。其中标记黑点的代表需要更新角度值,标记圆圈的代表需要更新向量值。
可以发现:
- 区间长度为 $1$ 的节点不需要更新角度值和向量值;
- 若某个节点所对应的区间包含要改变角度的位置 $(l_p < pos < r_p)$,则需要更新其向量值;
- 若某个节点需要更新向量值,且其右子节点没有更新角度值,则需要更新其角度值。
这样,每次更新便可以在 $O(\log n)$ 时间内完成,而根节点所对应向量的值就是要输出的结果。
参考代码
1 |
|