线段树之懒惰标记
最近在学习线段树的有关知识,期间遇到的重要的知识点和不错的习题,我会总结并记录下来,本系列将持续更新。当前的索引如下:
为什么引入懒惰标记?
懒惰标记的用处,就是更快地实现实现区间修改、区间查询。
考虑之前讲到的线段树。如果用线段树的单点修改,我们需要先改变叶子节点的值,然后不断地向上递归修改祖先节点直至到达根节点,时间复杂度最高可以到达 $O(n\log n)$ 的级别,这还只是单次操作,更别说有 $10^5$ 次指令的情况了。
该怎么实现?
其实就是用一个暂时不处理,等到需要用到的时候再进行处理的思想。
我们想,如果已经到达了属于答案区间范围内的节点,我们就直接对该节点进行一系列的操作,然后直接返回。这样,一定能保证本次区间更新的正确性。然而,区间更新不只一次,如果照刚刚那样更新而不进行任何后处理的话,那么该节点的子节点都未更新,势必会导致答案错误。于是,我们需要一种东西来记录下节点的更新信息,以便下次更新时处理。
所以引入一个名叫懒惰标记(lazytag) 的东西。之所以称其为 lazytag,是因为当我们引入懒惰标记后,我们不会去更新已经覆盖答案区间的子节点,只有在接下来的操作中我们才可能会用到该区间的子区间。所以这次操作就无需更新。区间更新的期望复杂度就降到了 $O(\log n)$ 的级别。
之前遇到的,只有单次修改、查询的情况,都是子区间向父区间传递信息,称之为 pushup。而这次将懒惰标记向下传递,不就是反过来,是父区间向子区间传递信息吗?我们将向下传递操作称为 pushdown。
线段树使用分治法,用递归进行实现。显然,子区间向父区间传递信息,应该在递归地操作子区间之后。而我们为了保证子区间的数据在操作其之前已被更新,就需要在递归操作之前,从父区间向子区间传递消息。
于是,以区间整体加上一个数的操作为例,就可以如此标记:
1 | /** |
我认为懒惰标记的使用,最重要的就是如何 pushdown 了,下面的几道题目很能说明问题。
【习题】线段树 2
提供一个序列,要求你维护三种操作:
- 将某区间每一个数乘上 $x$
- 将某区间每一个数加上 $x$
- 求出某区间每一个数的和
题解
在洛谷中作为一道模板题,这道题实在是太虐心了。不过不得不承认,做完以后对线段树和懒惰标记的理解深入了许多。
看了这题讨论区的题解,很多人说什么先乘后加,我也是想了挺久才弄懂。
于是考虑这样一个区间 $0$,和它的两个子区间 $1$ 和 $2$,如图:
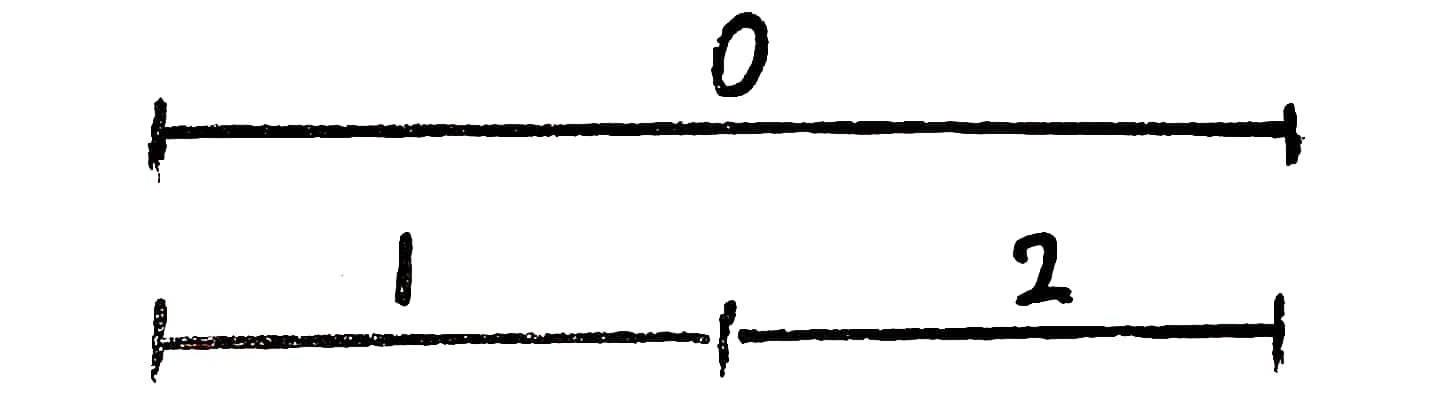
接着,我们记区间 $i$ 的区间的元素个数为 $span_i$ 、区间和为 $sum_i$ 、修改前的初始区间和为 $sum^\prime_i$ 、区间延迟加法的懒标记为 $lazyadd_i$ 、区间延迟乘法的懒标记为 $lazymul_i$ 。于是有以下初始情况,初始情况下,$lazyadd_i=0,lazymul_i=1$:
$$sum^\prime_0=sum^\prime_0\times\overbrace{1}^{lazymul_0} +\overbrace{0}^{lazyadd_0}\times span_0$$
考虑将 $0$ 区间,先整体加上 $3$,再整体乘以 $4$,于是有:
$$\begin{aligned}sum_0=&\,(sum^\prime_0\times\overbrace{1}^{lazymul_0} +\overbrace{0}^{lazyadd_0}\times span_0+3\times span_0)\times4\\=&\,(sum^\prime_0\times\overbrace{1}^{lazymul_0} +\overbrace{3}^{lazyadd_0}\times span_0)\times4\\=&\,sum^\prime_0\times\overbrace{4}^{lazymul_0}+\overbrace{12}^{lazyadd_0}\times span_0\end{aligned}$$
上式中转换的两步,分别对应了递归更新区间 “懒惰加法” 和 “懒惰乘法” 的代码(rs[p] - ls[p] 即 $span_p$):
1 | // 加法 |
接下来考虑父区间将信息传递给子区间的 pushdown 操作。以子区间 $1$ 为例,将父区间加上 $3$ 和乘以 $4$ 的信息传入。假设该区间本身就有懒惰标记,其初始值分别为 $lazyadd^\prime_1$ 和 $lazymul^\prime_1$,于是有:
$$\begin{aligned}sum_1&=\,(sum^\prime_1\times\overbrace{lazymul^\prime_1}^{lazymul_1}+\overbrace{lazyadd^\prime_1}^{lazyadd_1}\times span_1+3\times span_1)\times4\\&=\,[sum^\prime_1\times\overbrace{lazymul^\prime_1}^{lazymul_1} +\overbrace{(lazyadd^\prime_1+3)}^{lazyadd_1}\times span_1]\times4\\&=\, sum^\prime_1\times\overbrace{lazymul^\prime_1\times4}^{lazymul_1}+\overbrace{(lazyadd^\prime_1\times4+12)}^{lazyadd_1}\times span_1\\&=\, sum^\prime_1\times\overbrace{lazymul^\prime_1\times lazymul_0}^{lazymul_1} +\overbrace{(lazyadd^\prime_1\times lazymul_0+lazyadd_0)}^{lazyadd_1}\times span_1\end{aligned}$$
上式最后一步的转换比较关键,这样就和父区间建立起了联系。这对应了父区间向下传递的代码:
1 |
|
有了这些思路,代码自然就有了。
参考代码
1 |
|
【习题】市场
提供一个序列,要求你维护四种操作:
- 区间整体加上 $x$
- 区间的每一个数除以 $x$,并向下取整
- 查询区间最小值
- 查询区间和
题解
这题让我深刻地体会到了,自己是个大常数选手。同一段代码别人用 $2500{\rm ms}$,我的要用 $3300{\rm ms}$ 。代码常数的差别,不是一两处修改就能赶上来的,有些习惯让大常数的代码无处不在… 说了一些废话。
这四种操作,我认为第二种是最重要的,其它都只是摆设罢了。
除以一个数容易想,维护两个懒惰标记,一个对应加法、一个对应除法就行了。可对于整除来说,这方法完全行不通。于是想到,很接近的数,比如 $9$ 和 $10$,在除以 $5$ 并向下取整后将变为 $1$ 和 $2$ 。相当于给两个数都减去了 $8$ 。于是,区间整除就变成了区间减法。
判断整个区间的数是否具备将整除转为区间减法的条件,需要记录下区间的最大值和最小值。一般来说只有最大值等于最小值,也就是区间数字都相同时符合条件。但比如说刚才 $9$ 和 $10$ 的例子,比较大的数能够被除数整除,则最小值可以比最大值小 $1$ 。
参考代码
1 |
|